Plotting Simple Curves

Plotting Simple Curves#

Import and Settings#

We will import NumPy and matplotlib. In addition, we will also start with some customised layout for the plot.

import numpy as np
import matplotlib.pyplot as plt

Partitioning the real line#

In order to plot a curve, we need a set of \(x\) values and the corresponding \(y\) values. Since \(x\) is the independent variable, we need to first generate a list of values for \(x\).

In NumPy:

x = np.linspace(0, 1, 11)
x

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])

Curves#

We shall plot several curves, starting from simple curves to more complex ones. In this process, we will also learn how to add simple annotations to the plot.

Curve-1#

Plot \(y = x\) for \(x \in [0, 1]\). Sample \(10\) equally spaced points in this interval, inclusive of endpoints.

In NumPy:

x = np.linspace(0, 1, 10)
y = x
plt.plot(x, y)

[<matplotlib.lines.Line2D at 0x7fd9f0c34e20>]
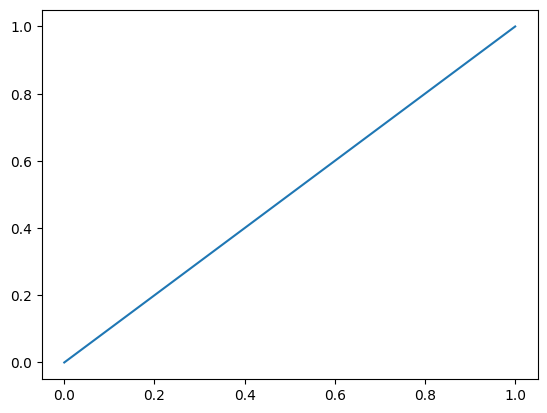
../_images/5aae73ad2445357cbe0df81f29bc52866583a2ecd6fdd68808af9ffca31f9098.png

If we also wish to visualise the points, we can add a scatter plot along with the line plot.

x = np.linspace(0, 1, 10)
y = x
plt.plot(x, y) # ; is added to suprress the output

[<matplotlib.lines.Line2D at 0x7fd9f0cf7fd0>]
../_images/5aae73ad2445357cbe0df81f29bc52866583a2ecd6fdd68808af9ffca31f9098.png

Curve-2#

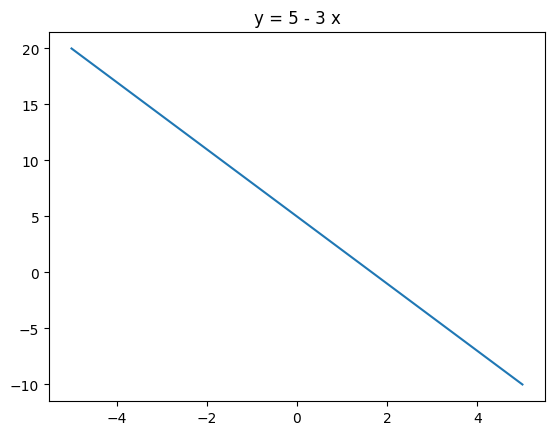
Plot \(y = 5 - 3x\) for \(x \in [-5, 5]\). Sample \(20\) equally spaced points in this interval, inclusive of endpoints. Add a title to the plot which has the equation of the curve.

x = np.linspace(-5, 5, 20)
y = 5 - 3 * x
plt.plot(x, y)
plt.title('y = 5 - 3 x');
../_images/74b8016ffa4fb0d88fd38add9ddb8a3823be6eb6d12df965e8773e5b7c098035.png

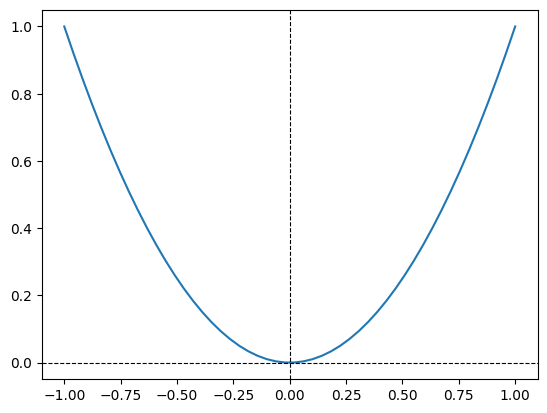
Curve-3#

Plot \(y = x^2\) for \(x \in [-1, 1]\). Try out four different samples for x:

  • \(5\) equally spaced points in this interval, endpoints inclusive

  • \(10\) equally spaced points in this interval, endpoints inclusive

  • \(20\) equally spaced points in this interval, endpoints inclusive

  • \(50\) equally spaced points in this interval, endpoints inclusive

Observe the differences in these four plots. Which one would you choose? Add the equation of the curve as the title of the plot. Also add the x and y-axis to the plot.

x = np.linspace(-1, 1)
y = x ** 2
plt.plot(x, y)
plt.axhline(color = 'black', linestyle = '--', linewidth = 0.8)
plt.axvline(color = 'black', linestyle = '--', linewidth = 0.8);
../_images/22e414f6b423a80af7355fbdc3829a60c3885da15012c9d4068653981ce1c2b0.png

Curve-4#

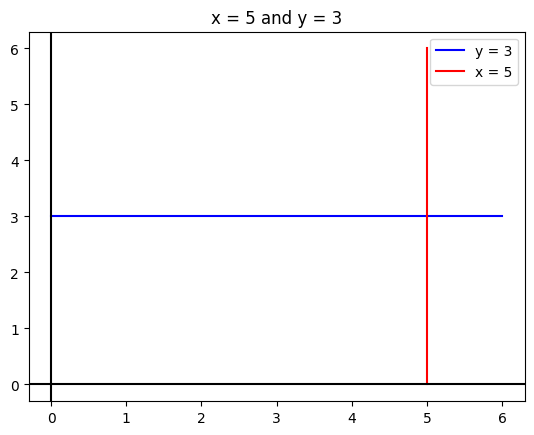
Plot \(y = 3\) and \(x = 5\) on the same plot. Color the first one green and the second one red. Limit your plot to the region \(x \in [0, 6]\) and \(y \in [0, 6]\).

  • Label the x and the y axes.

  • Add a suitable title.

  • Add a legend.

# y = 3
x = np.linspace(0, 6, 2)
y = np.ones(2) * 3
plt.plot(x, y, color = 'blue', label = 'y = 3')

# x = 5
x = np.ones(2) * 5
y = np.linspace(0, 6, 2)
plt.plot(x, y, color = 'red', label = 'x = 5')

plt.legend()
plt.title('x = 5 and y = 3')
plt.axhline(color = 'black')
plt.axvline(color = 'black');
../_images/c2524ac323a2670f8f10ceaedf09d7d13c874a7e1ab98f71d34b7948dbe3e012.png

Subplots#

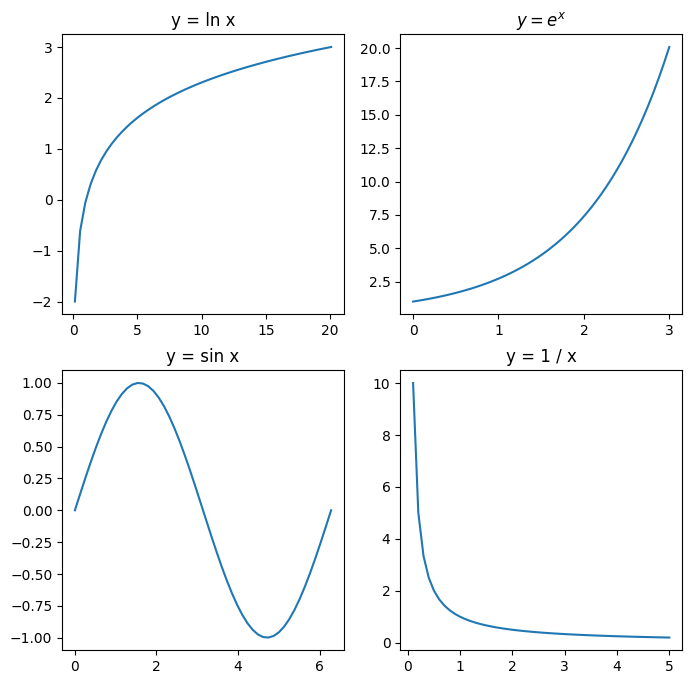
Sometimes we may have to plot multiple objects, each in a separate plot. Plot the following curves, each in a separe plot:

  • \(y = \ln x, \quad x \in \left( \cfrac{1}{e^2}, e^3 \right)\)

  • \(y = e^x, \quad x \in (0, 3)\)

  • \(y = \sin x, \quad x \in [0, 2 \pi]\)

  • \(y = \cfrac{1}{x}, \quad x \in (0, 5)\)

Title each curve appropriately.

# rcParams is like a dict
# controls various configurations
plt.rcParams['figure.figsize'] = [8, 8]
plt.rcParams['font.size'] = 10

# Plot-1
plt.subplot(2, 2, 1)
x = np.linspace(1 / np.e ** 2, np.e ** 3)
y = np.log(x)
plt.plot(x, y)
plt.title('y = ln x')

# Plot-2
plt.subplot(2, 2, 2)
x = np.linspace(0, 3)
y = np.exp(x)
plt.plot(x, y)
plt.title('$y = e^x$')

# Plot-3
plt.subplot(2, 2, 3)
x = np.linspace(0, 2 * np.pi)
y = np.sin(x)
plt.plot(x, y)
plt.title('y = sin x')

# Plot-4
plt.subplot(2, 2, 4)
x = np.linspace(0.1, 5)
y = 1 / x
plt.plot(x, y)
plt.title('y = 1 / x')

Text(0.5, 1.0, 'y = 1 / x')
../_images/6fadb198f4c4bece5a674cf0fb4d8f4cb9f1d4e468b4642d98296867fb5344a7.png
Contents