OPPE | T2-2024 | Solutions

OPPE | T2-2024 | Solutions#

Instructions#

There are \(17\) NAT questions with marks distributed as \(1 \times 2 + 16 \times 3 = 50\).
Answers to all questions are going to be integers.
Solve the problem in the colab and enter the answer in the portal.
Always run the data-cell before running the solution cell.
In questions where a data-matrix \(\mathbf{X}\) and label-vector \(\mathbf{y}\) are mentioned, the data-cell will have the corresponding entries as X and y.
All other vectors, matrices and scalars necessary for solving the problem will be given in the data-cell. They will have the same name as the ones mentioned in the problem statement.
round is a function that can be used to find the nearest integer. For example, round(1.2) == 1 and round(1.9) == 2.

Notation#

The data-matrix in all problems will be of shape \(d \times n\), where \(d\) is the number of features and \(n\) is the number of data-points.
If \(\mathbf{x} = (1, 2, 3)\) is a vector, \(1, 2\) and \(3\) are termed the components of \(\mathbf{x}\). The sum of the components of \(\mathbf{x}\) is \(6\).
The norm of a vector \(\mathbf{x}\) is the Euclidean norm (\(L_2\)) by default. This is the only norm used in this exam.
All vectors will be represented as one-dimensional NumPy arrays. All matrices will be represented as two-dimensional NumPy arrays.

import numpy as np
import matplotlib.pyplot as plt

Question-1 [2 marks]#

\(\mathbf{X}\) is a data-matrix. If \(\boldsymbol{\mu}\) is the mean of the data-points, find the norm of \(\boldsymbol{\mu}\) and enter the nearest integer as your answer.

# DATA CELL
# DO NOT EDIT THIS
rng = np.random.default_rng(seed = 1001)
d = rng.integers(2, 10)
n = rng.integers(40, 50)
X = rng.integers(-5, 10, (d, n))

# Solution
# Run the data cell before running this
mu = X.mean(axis = 1)
round(np.linalg.norm(mu))

Question-2 [3 marks]#

\(\mathbf{X}\) is a data-matrix. Find the number of data-points whose norm is at least \(k\).

# DATA CELL
# DO NOT EDIT THIS
rng = np.random.default_rng(seed = 1002)
k = rng.integers(10, 20)
d = rng.integers(5, 10)
n = rng.integers(50, 100)
X = rng.integers(-10, 10, (d, n))

# Solution
# Run the data cell before running this
np.where(
    np.linalg.norm(X, axis = 0) >= k,
    1,
    0
).sum()

Question-3 [3 marks]#

Consider a matrix \(\mathbf{A}\) of shape \(m \times n\). Find the trace of the matrix \(\mathbf{A}^T \mathbf{A}\), where the trace is the sum of the diagonal elements. Enter the nearest integer as the answer.

# DATA CELL
# DO NOT EDIT THIS
rng = np.random.default_rng(seed = 1003)
m, n = rng.integers(50, 100, 2)
A = rng.integers(-1, 2, (m, n))

# Solution
# Run the data cell before running this
M = A.T @ A
round(
    sum(
        [M[i][i] for i in range(M.shape[0])]
    )
)

Question-4 [3 marks]#

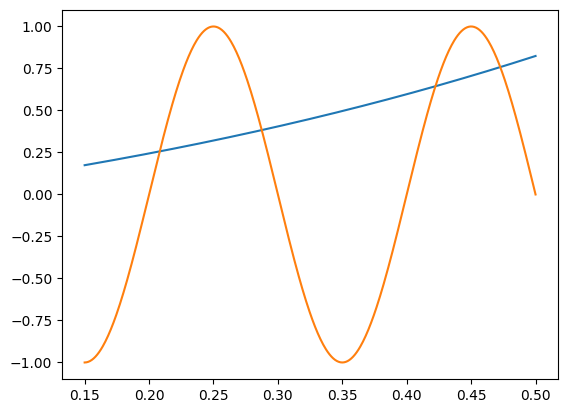
Consider the curves:

\[\begin{split} \begin{aligned} y &= xe^{x}\\\\ y &= \sin(10 \pi x) \end{aligned} \end{split}\]

Find the number of points at which these two curves intersect in the interval \(0.15 \leqslant x \leqslant 0.5\).

# Solution
x = np.linspace(0.15, 0.5, 500)
plt.plot(x, x * np.exp(x))
plt.plot(x, np.sin(10 * np.pi * x))
print(4)

../_images/22cbde5ca8e1accc464eabcdc9e165a7ca238ae83219e6d25a6ae60e5d72b69d.png

Question-5 [3 marks]#

Consider the system of equations \(\mathbf{Ax} = \mathbf{b}\), where:

\[\begin{split} \mathbf{A} = \begin{bmatrix} 1 & 2 & -1 & 3\\ 0 & 1 & 2 & -1\\ 1 & -2 & 3 & 1\\ 0 & -1 & -1 & 2 \end{bmatrix}, \quad \mathbf{b} = \begin{bmatrix} 1\\ 2\\ -1\\ 0 \end{bmatrix} \end{split}\]

If \(A\) is invertible, find the solution to this system, and enter the sum of the components of the solution as the answer. Your answer should be an integer.

# Solution
A = np.array([
    [1, 2, -1, 3],
    [0, 1, 2, -1],
    [1, -2, 3, 1],
    [0, -1, -1, 2]
])
b = np.array([1, 2, -1, 0])
assert np.linalg.matrix_rank(A) == A.shape[0]
x = np.linalg.inv(A) @ b
x.sum()

0.0

Question-6 [3 marks]#

Let \(\mathbf{w}\) be the weight vector of a linear classifier trained on a dataset for a binary classification problem with data-matrix \(\mathbf{X}\) and label vector \(\mathbf{y}\). The predicted label for a data-point \(\mathbf{x}\) defined as:

\[\begin{split} \widehat{y} = \begin{cases} 1,& \mathbf{w}^{T} \mathbf{x} \geqslant 0,\\ 0,& \text{otherwise} \end{cases} \end{split}\]

Find the predicted label vector and enter the sum of the components of the predicted label vector as the answer.

# DATA CELL
# DO NOT EDIT THIS
rng = np.random.default_rng(seed = 1006)
d = rng.integers(3, 6)
n = rng.integers(40, 60)
if n % 2 != 0: n += 1
X = rng.uniform(-2, 2, (d, n))
y = np.concatenate(
    (np.ones(n // 2),
    np.zeros(n // 2))
)
w = rng.uniform(-5, 5, d)

# Solution
# Run the data cell before running this
y_hat = np.where(w @ X >= 0, 1, 0)
y_hat.sum()

Common data for questions (7) to (10)#

Consider the following dataset for a binary classification problem. The data-matrix \(\mathbf{X}\) and the label vector \(\mathbf{y}\) are given below.

# DATA CELL
# DO NOT EDIT THIS
X = np.array([
    [2, 2, 2, 3, -2, -2, -5, -3],
    [0, 1, -1, 0, 0, -3, 3, -1]
])
y = np.array(
    [-1, -1, -1, -1, 1, 1, 1, 1]
)

Question-7 [3 marks]#

Train a perceptron algorithm on this dataset. Cycle through the data-points from left to right, that is, \(i = 0\) to \(i = n - 1\). Make sure to strictly follow this cycle. If you make an update at data-point \(j\), proceed to data-point \(j + 1\) in the next iteration. Once you reach \(n - 1\), cycle back to \(0\).

Find the sum of the components of the weight vector and enter the nearest integer as your answer.

# Solution
# Run the data cell before running this
d, n = X.shape
i = cycle = 0
w = np.zeros(d)
while cycle != n:
    y_hat = 1 if X[:, i] @ w >= 1 else -1
    if y_hat != y[i]:
        w += X[:, i] * y[i]
        cycle = 0
    else:
        cycle += 1
    i += 1
    if i == n:
        i = 0
w.sum()

-2.0

Question-8 [3 marks]#

In the context of hard-margin SVM, find the optimal \(\boldsymbol{\alpha}^{*}\) by solving the following dual optimization problem.

\[ \begin{equation*} \underset{\boldsymbol{\alpha} \geqslant \mathbf{0}}{\max}\ \ \ \ \boldsymbol{\alpha}^{T}\mathbf{1} -\frac{1}{2}\boldsymbol{\alpha}^{T}\mathbf{Y}^{T}\mathbf{X}^{T}\mathbf{XY} \boldsymbol{\alpha} \end{equation*} \]

If the sum of the components of \(\boldsymbol{\alpha}^{*}\) is \(s\), find \(\cfrac{1}{s}\) and enter the nearest integer to \(\cfrac{1}{s}\) as the answer.

# Solution
# Run the data cell before running this
from scipy.optimize import minimize
from scipy.optimize import Bounds

Y = np.diag(y)
def f(alpha):
    return (
        0.5 * alpha @ Y.T @ X.T @ X @ Y @ alpha
        - alpha.sum()
    )
res = minimize(
    f, x0 = np.zeros(n),
    bounds = Bounds(0, np.inf)
)
alpha_star = res.x
round(1 / alpha_star.sum())

Question-9 [3 marks]#

Find the optimal weight vector \(\mathbf{w}^{*}\). If the sum of the components of \(\mathbf{w}^{*}\) is \(s\), find \(\cfrac{1}{s}\) and enter the nearest integer to \(\cfrac{1}{s}\) as the answer.

# Solution
w_star = X @ Y @ alpha_star
round(1 / w_star.sum())

-2

Question-10 [3 marks]#

Find the number of support vectors.

# Solution
(alpha_star > 0).sum()

Common data for questions (11) and (12)#

Consider a data-matrix \(\mathbf{X}\). Mean center it and perform linear PCA.

# DATA CELL
# DO NOT EDIT THIS
X = np.array([
    [7, 5, -6, -11, 14.4, -2.8],
    [10.5, 7.5, -9, -16.5, 21.6, -4.2],
    [21, 15, -18, -33, 43.2, -8.4]
]).astype(np.float64)

# Solution
# Run the data cell before running this
d, n = X.shape
X -= X.mean(axis = 1).reshape(d, 1)
C = X @ X.T / n
eigval, eigvec = np.linalg.eigh(C)
var = np.flip(eigval)
pcs = np.flip(eigvec, axis = 1)

Question-11 [3 marks]#

If the first PC is \(\mathbf{w}_1\), let the sum of the components of \(\mathbf{w}_1\) be \(a\). Find the absolute value of \(7a\) and enter the nearest integer as your answer.

# Solution
round(np.abs(pcs[:, 0].sum() * 7))

Question-12 [3 marks]#

Find the variance along the first PC. Enter the nearest integer as your answer.

# Solution
round(var[0])

Question-13 [3 marks]#

Find the sum of the variances along the second and third PC. Enter the nearest integer as your answer.

# Solution
round(var[1:].sum())

Common data for questions (14) to (16)#

Consider a dataset \(\mathbf{X}\) for a clustering problem. Start with the initial means as \(\boldsymbol{\mu}_1 = (2, 3, 5)\) and \(\boldsymbol{\mu}_2 = (-3, -5, -7)\) and run K-means with \(k = 2\).

# DATA CELL
# DO NOT EDIT THIS
X = np.array([
    [-8.2, 3.2, -5.1, 4., -7, 8.1, -2],
    [-10.1, 4.1, -3.3, 2., -5, 6.2, -5],
    [-3.4, 4.9, -3, 2., -5, 6.5, -5.3]
])

# Solution
mus = np.array([
    [2., -3.],
    [3., -5.],
    [5., -7.]
])
d, n = X.shape

z_prev = np.ones(n)
z = np.zeros(n)
k = 2
while not np.array_equal(z_prev, z):
    z_prev = z.copy()
    for i in range(n):
        dsq = (mus - X[:, i].reshape(d, 1)) ** 2
        z[i] = np.argmin(dsq.sum(axis = 0))

    for j in range(k):
        if np.any(z == j):
            mus[:, j] = X[:, z == j].mean(axis = 1)
mus

array([[ 5.1       , -5.575     ],
       [ 4.1       , -5.85      ],
       [ 4.46666667, -4.175     ]])

Question-14 [3 marks]#

Find the norm of the final mean \(\boldsymbol{\mu}_1\). Enter the nearest integer as your answer.

# Solution
round(np.linalg.norm(mus[:, 0]))

Question-15 [3 marks]#

Find the norm of the final mean \(\boldsymbol{\mu}_2\). Enter the nearest integer as your answer.

round(np.linalg.norm(mus[:, 1]))

Question-16 [3 marks]#

Find the cluster to which the data-point \((0, 1, 2)\) belongs. Enter \(1\) if it is closer to \(\boldsymbol{\mu}_1\) than \(\boldsymbol{\mu}_2\) and \(2\) otherwise.

x = np.array([0, 1, 2])
dsq = (mus - x.reshape(d, 1))  ** 2
np.argmin(dsq.sum(axis = 0)) + 1

Question-17 [3 marks]#

Fit a linear regression model on the dataset \((\mathbf{X}, \mathbf{y})\) and find the optimal weight vector \(\mathbf{w}^{*}\) using the normal equations. Enter the nearest integer to the sum of the components of \(\mathbf{w}^{*}\) as the answer.

# DATA CELL
# DO NOT EDIT THIS
X = np.array([
    [1., -1., 3., -2., 1.],
    [0., -2., 1., 0., 3.],
    [-2., 1., 0., 1., 2.],
    [1., -2., 3., -1., 4.]
])
y = np.array(
    [3.1, 4.9, -2.5, 10.3, -4.2]
)

d, n = X.shape
w = np.linalg.pinv(X.T) @ y
round(w.sum())

-9